Note
Go to the end to download the full example code
Convergence study (spatial refinement)#
This example shows one possible implementation of how to do a convergence study. It uses the project file from the following benchmark with multiple discretizations to evaluate the accuracy of the numerical solutions. ogs: elliptic neumann benchmark
Here is some theoretical background for the topic of grid convergence:
At least three meshes of increasing refinement are required for the convergence study. The three finest meshes are used to calculated the Richardson extrapolation. The third coarsest mesh will be used for the topology to evaluate the results. Its nodes should be shared by the finer meshes, otherwise interpolation will influence the results. With unstructured grids this can be achieved as well with refinement by splitting.
The results to analyze are generated on the fly with the following code. If you are only interested in the convergence study, please skip to Hydraulic pressure convergence.
First, the required packages are imported and an output directory is created:
from pathlib import Path
from shutil import rmtree
from tempfile import mkdtemp
from IPython.display import HTML
from ogs6py import ogs
from ogstools import meshlib, meshplotlib, msh2vtu, propertylib, workflow
from ogstools.studies import convergence
from ogstools.studies.convergence.examples import (
steady_state_diffusion_analytical_solution,
)
meshplotlib.setup.reset()
temp_dir = Path(mkdtemp(suffix="steady_state_diffusion"))
report_name = str(temp_dir / "report.ipynb")
result_paths = []
The meshes and their boundaries are generated easily via gmsh and
ogstools.msh2vtu.
Then we run the different simulations with increasingly fine spatial
discretization via ogs6py and store the results for the convergence study.
refinements = 6
edge_cells = [2**i for i in range(refinements)]
for n_edge_cells in edge_cells:
msh_path = temp_dir / "square.msh"
meshlib.gmsh_meshing.rect(
n_edge_cells=n_edge_cells, structured_grid=True, out_name=msh_path
)
msh2vtu.msh2vtu(
input_filename=msh_path, output_path=temp_dir, log_level="ERROR"
)
model = ogs.OGS(
PROJECT_FILE=temp_dir / "default.prj",
INPUT_FILE=convergence.examples.steady_state_diffusion_prj,
)
prefix = "steady_state_diffusion_" + str(n_edge_cells)
model.replace_text(prefix, ".//prefix")
model.write_input()
ogs_args = f"-m {temp_dir} -o {temp_dir}"
model.run_model(write_logs=False, args=ogs_args)
result_paths += [str(temp_dir / (prefix + ".pvd"))]
OGS finished with project file /tmp/tmptjl43l8bsteady_state_diffusion/default.prj.
Execution took 0.12485575675964355 s
OGS finished with project file /tmp/tmptjl43l8bsteady_state_diffusion/default.prj.
Execution took 0.13041996955871582 s
OGS finished with project file /tmp/tmptjl43l8bsteady_state_diffusion/default.prj.
Execution took 0.13088107109069824 s
OGS finished with project file /tmp/tmptjl43l8bsteady_state_diffusion/default.prj.
Execution took 0.14280962944030762 s
OGS finished with project file /tmp/tmptjl43l8bsteady_state_diffusion/default.prj.
Execution took 0.1478884220123291 s
OGS finished with project file /tmp/tmptjl43l8bsteady_state_diffusion/default.prj.
Execution took 0.14978790283203125 s
Here we calculate the analytical solution on one of the meshes:
analytical_solution_path = temp_dir / "analytical_solution.vtu"
solution = steady_state_diffusion_analytical_solution(
meshlib.MeshSeries(result_paths[-1]).read(0)
)
meshplotlib.setup.show_element_edges = True
fig = meshplotlib.plot(solution, propertylib.presets.hydraulic_height)
solution.save(analytical_solution_path)
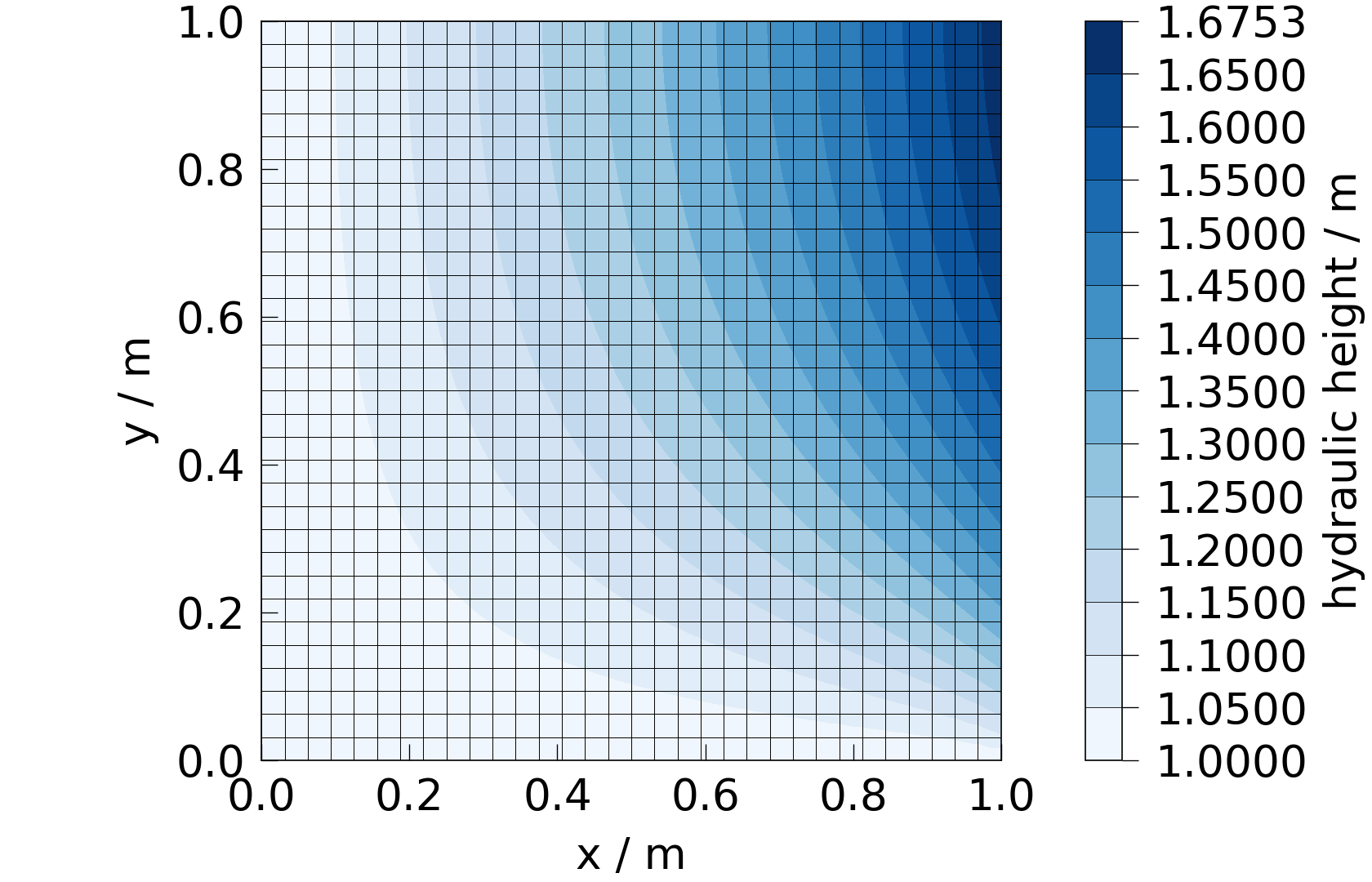
Hydraulic pressure convergence#
The pressure field of this model is converging well. The convergence ratio is approximately 1 on the whole mesh and looking at the relative errors we see a quadratic convergence behavior.
convergence.run_convergence_study(
output_name=report_name,
mesh_paths=result_paths,
property_name="hydraulic_height",
timevalue=1,
refinement_ratio=2.0,
reference_solution_path=str(analytical_solution_path),
)
HTML(workflow.jupyter_to_html(report_name, show_input=False))
Darcy velocity convergence#
For the velocity we some discrepancy of the convergence ratio in the bottom right corner. Thus we know, at these points the mesh isn’t properly converging (at least for the velocity field). We see, that in the bottom right corner, the velocity magnitude seems to be steadily increasing, which is also reflected in the Richardson extrapolation, which shows an anomalous high value in this spot, hinting at a singularity there. This is explained by the notion in the benchmark’s documentation of “incompatible boundary conditions imposed on the bottom right corner of the domain.” Regardless of this, the benchmark gives a convergent solution for the pressure field. The code cells from the templated notebook are show here for transparency.
convergence.run_convergence_study(
output_name=report_name,
mesh_paths=result_paths,
property_name="velocity",
timevalue=1,
refinement_ratio=2.0,
)
HTML(workflow.jupyter_to_html(report_name, show_input=True))
Total running time of the script: (0 minutes 17.924 seconds)