Note
Go to the end to download the full example code.
Component-transport model - conversion and simulation#
Section author: Julian Heinze (Helmholtz Centre for Environmental Research GmbH - UFZ)
In this example we show how a simple mass transport FEFLOW model can be converted to a pyvista.UnstructuredGrid and then be simulated in OGS with the component transport process.
Necessary imports
import tempfile
import xml.etree.ElementTree as ET
from pathlib import Path
import ifm_contrib as ifm
import matplotlib.pyplot as plt
from ogs6py import ogs
import ogstools.meshplotlib as mpl
from ogstools.examples import feflow_model_2D_CT_t_560
from ogstools.feflowlib import (
component_transport,
convert_properties_mesh,
get_material_properties_of_CT_model,
get_species,
setup_prj_file,
write_point_boundary_conditions,
)
from ogstools.meshlib import MeshSeries
from ogstools.propertylib import Scalar
1. Load a FEFLOW model (.fem) as a FEFLOW document, convert and save it. More details on
how the conversion function works can be found here: ogstools.feflowlib.convert_properties_mesh.
feflow_model = ifm.loadDocument(str(feflow_model_2D_CT_t_560))
feflow_pv_mesh = convert_properties_mesh(feflow_model)
temp_dir = Path(tempfile.mkdtemp("feflow_test_simulation"))
feflow_mesh_file = temp_dir / "2D_CT_model.vtu"
feflow_pv_mesh.save(feflow_mesh_file)
feflow_concentration = Scalar(
data_name="single_species_P_CONC", data_unit="mg/l", output_unit="mg/l"
)
# The original mesh is clipped to focus on the relevant part of it, where concentration is larger
# than 1e-9 mg/l. The rest of the mesh has concentration values of 0.
mpl.plot(
feflow_pv_mesh.clip_scalar(
scalars="single_species_P_CONC", invert=False, value=1.0e-9
),
feflow_concentration,
)
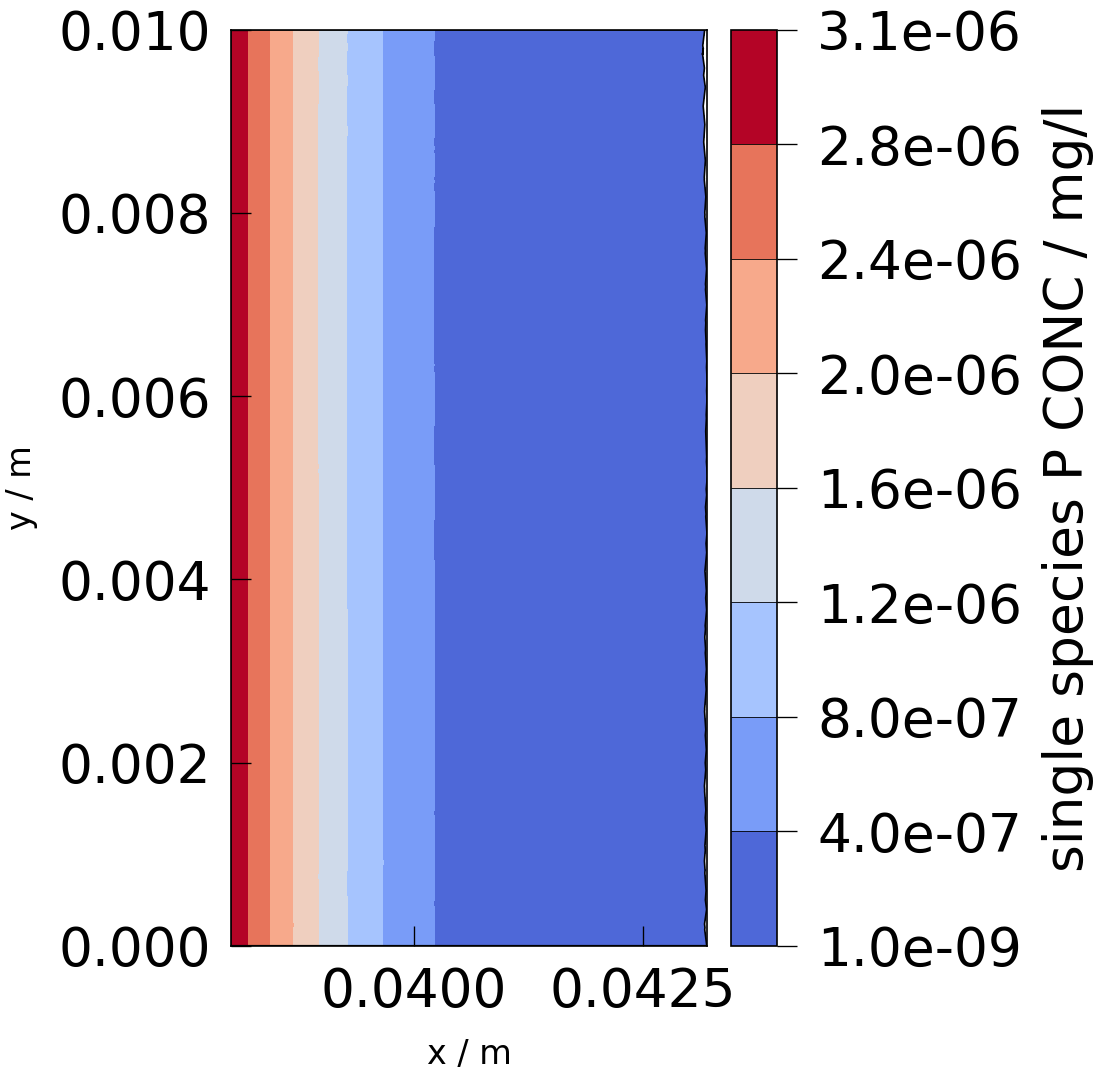
<Figure size 1099.71x1080 with 2 Axes>
Save the point boundary conditions (see:
ogstools.feflowlib.write_point_boundary_conditions).
write_point_boundary_conditions(temp_dir, feflow_pv_mesh)
Setup a prj-file (see:
ogstools.feflowlib.setup_prj_file) to run a OGS-simulation.
path_prjfile = feflow_mesh_file.with_suffix(".prj")
prjfile = ogs.OGS(PROJECT_FILE=path_prjfile)
species = get_species(feflow_pv_mesh)
CT_model = component_transport(
saving_path=temp_dir / "sim_2D_CT_model",
species=species,
model=prjfile,
dimension=2,
fixed_out_times=[48384000],
)
# Include the mesh specific configurations to the template.
model = setup_prj_file(
bulk_mesh_path=feflow_mesh_file,
mesh=feflow_pv_mesh,
material_properties=get_material_properties_of_CT_model(feflow_pv_mesh),
process="component transport",
species_list=species,
model=CT_model,
initial_time=0,
end_time=4.8384e07,
time_stepping=list(zip([10] * 8, [8.64 * 10**i for i in range(8)])),
max_iter=6,
rel_tol=1e-14,
)
# The model must be written before it can be run.
model.write_input(path_prjfile)
# Print the prj-file as an example.
ET.dump(ET.parse(path_prjfile))
<OpenGeoSysProject>
<meshes>
<mesh>2D_CT_model.vtu</mesh>
<mesh>single_species_P_BC_MASS.vtu</mesh>
</meshes>
<processes>
<process>
<name>CT</name>
<type>ComponentTransport</type>
<coupling_scheme>staggered</coupling_scheme>
<integration_order>2</integration_order>
<specific_body_force>0 0</specific_body_force>
<process_variables>
<pressure>HEAD_OGS</pressure>
<concentration>single_species</concentration>
</process_variables>
</process>
</processes>
<media>
<medium id="0">
<phases>
<phase>
<type>AqueousLiquid</type>
<properties>
<property>
<name>viscosity</name>
<type>Constant</type>
<value>1</value>
</property>
<property>
<name>density</name>
<type>Constant</type>
<value>1</value>
</property>
</properties>
<components>
<component>
<name>single_species</name>
<properties>
<property>
<name>decay_rate</name>
<type>Constant</type>
<value>0.0</value>
</property>
<property>
<name>pore_diffusion</name>
<type>Constant</type>
<value>3.5999998241701783e-10</value>
</property>
<property>
<name>retardation_factor</name>
<type>Constant</type>
<value>16441.72737282367</value>
</property>
</properties>
</component>
</components>
</phase>
</phases>
<properties>
<property>
<name>porosity</name>
<type>Constant</type>
<value>0.10999999940395355</value>
</property>
<property>
<name>longitudinal_dispersivity</name>
<type>Constant</type>
<value>0.0</value>
</property>
<property>
<name>transversal_dispersivity</name>
<type>Constant</type>
<value>0.0</value>
</property>
<property>
<name>permeability</name>
<type>Constant</type>
<value>1.1574074074074073e-05</value>
</property>
</properties>
</medium>
</media>
<time_loop>
<processes>
<process ref="CT">
<nonlinear_solver>basic_picard</nonlinear_solver>
<convergence_criterion>
<type>DeltaX</type>
<norm_type>NORM2</norm_type>
<reltol>1e-6</reltol>
</convergence_criterion>
<time_discretization>
<type>BackwardEuler</type>
</time_discretization>
<time_stepping>
<type>FixedTimeStepping</type>
<t_initial>0</t_initial>
<t_end>48384000.0</t_end>
<timesteps>
<pair>
<repeat>10</repeat>
<delta_t>8.64</delta_t>
</pair>
<pair>
<repeat>10</repeat>
<delta_t>86.4</delta_t>
</pair>
<pair>
<repeat>10</repeat>
<delta_t>864.0</delta_t>
</pair>
<pair>
<repeat>10</repeat>
<delta_t>8640.0</delta_t>
</pair>
<pair>
<repeat>10</repeat>
<delta_t>86400.0</delta_t>
</pair>
<pair>
<repeat>10</repeat>
<delta_t>864000.0</delta_t>
</pair>
<pair>
<repeat>10</repeat>
<delta_t>8640000.0</delta_t>
</pair>
<pair>
<repeat>10</repeat>
<delta_t>86400000.0</delta_t>
</pair>
</timesteps>
</time_stepping>
</process>
<process ref="CT">
<nonlinear_solver>basic_picard</nonlinear_solver>
<convergence_criterion>
<type>DeltaX</type>
<norm_type>NORM2</norm_type>
<reltol>1e-6</reltol>
</convergence_criterion>
<time_discretization>
<type>BackwardEuler</type>
</time_discretization>
<time_stepping>
<type>FixedTimeStepping</type>
<t_initial>0</t_initial>
<t_end>48384000.0</t_end>
<timesteps>
<pair>
<repeat>10</repeat>
<delta_t>8.64</delta_t>
</pair>
<pair>
<repeat>10</repeat>
<delta_t>86.4</delta_t>
</pair>
<pair>
<repeat>10</repeat>
<delta_t>864.0</delta_t>
</pair>
<pair>
<repeat>10</repeat>
<delta_t>8640.0</delta_t>
</pair>
<pair>
<repeat>10</repeat>
<delta_t>86400.0</delta_t>
</pair>
<pair>
<repeat>10</repeat>
<delta_t>864000.0</delta_t>
</pair>
<pair>
<repeat>10</repeat>
<delta_t>8640000.0</delta_t>
</pair>
<pair>
<repeat>10</repeat>
<delta_t>86400000.0</delta_t>
</pair>
</timesteps>
</time_stepping>
</process>
</processes>
<output>
<type>VTK</type>
<prefix>/tmp/tmp42n7r7cxfeflow_test_simulation/sim_2D_CT_model</prefix>
<timesteps>
<pair>
<repeat>1</repeat>
<each_steps>48384000</each_steps>
</pair>
</timesteps>
<variables>
<variable>single_species</variable>
<variable>HEAD_OGS</variable>
</variables>
<fixed_output_times>48384000</fixed_output_times>
</output>
<global_process_coupling>
<max_iter>6</max_iter>
<convergence_criteria>
<convergence_criterion>
<type>DeltaX</type>
<norm_type>NORM2</norm_type>
<reltol>1e-14</reltol>
</convergence_criterion>
<convergence_criterion>
<type>DeltaX</type>
<norm_type>NORM2</norm_type>
<reltol>1e-14</reltol>
</convergence_criterion>
</convergence_criteria>
</global_process_coupling>
</time_loop>
<parameters>
<parameter>
<name>C0</name>
<type>Constant</type>
<value>0</value>
</parameter>
<parameter>
<name>p0</name>
<type>Constant</type>
<value>0</value>
</parameter>
<parameter>
<name>single_species_P_BC_MASS</name>
<type>MeshNode</type>
<mesh>single_species_P_BC_MASS</mesh>
<field_name>single_species_P_BC_MASS</field_name>
</parameter>
</parameters>
<process_variables>
<process_variable>
<name>single_species</name>
<components>1</components>
<order>1</order>
<initial_condition>C0</initial_condition>
<boundary_conditions>
<boundary_condition>
<type>Dirichlet</type>
<mesh>single_species_P_BC_MASS</mesh>
<parameter>single_species_P_BC_MASS</parameter>
</boundary_condition>
</boundary_conditions>
</process_variable>
<process_variable>
<name>HEAD_OGS</name>
<components>1</components>
<order>1</order>
<initial_condition>p0</initial_condition>
</process_variable>
</process_variables>
<nonlinear_solvers>
<nonlinear_solver>
<name>basic_picard</name>
<type>Picard</type>
<max_iter>10</max_iter>
<linear_solver>general_linear_solver</linear_solver>
</nonlinear_solver>
</nonlinear_solvers>
<linear_solvers>
<linear_solver>
<name>general_linear_solver</name>
<lis>-i bicgstab -p ilut -tol 1e-10 -maxiter 10000</lis>
<eigen>
<solver_type>CG</solver_type>
<precon_type>DIAGONAL</precon_type>
<max_iteration_step>100000</max_iteration_step>
<error_tolerance>1e-20</error_tolerance>
</eigen>
<petsc>
<prefix>ct</prefix>
<parameters>-ct_ksp_type bcgs -ct_pc_type bjacobi -ct_ksp_rtol 1e-16 -ct_ksp_max_it 10000</parameters>
</petsc>
</linear_solver>
</linear_solvers>
</OpenGeoSysProject>
Run the model.
model.run_model(logfile=temp_dir / "out.log")
OGS finished with project file /tmp/tmp42n7r7cxfeflow_test_simulation/2D_CT_model.prj.
Execution took 2.9460339546203613 s
Read the results along a line on the upper edge of the mesh parallel to the x-axis and plot them.
ms = MeshSeries(temp_dir / "sim_2D_CT_model.pvd")
# Read the last timestep:
ogs_sim_res = ms.read(ms.timesteps[-1])
"""
It is also possible to read the file directly with pyvista:
ogs_sim_res = pv.read(
temp_dir / "sim_2D_CT_model_ts_65_t_48384000.000000.vtu"
)
"""
start_line = (0.038 + 1.0e-8, 0.005, 0)
end_line = (0.045, 0.005, 0)
ogs_line = ogs_sim_res.sample_over_line(start_line, end_line, resolution=100)
feflow_line = feflow_pv_mesh.sample_over_line(
start_line, end_line, resolution=100
)
plt.rcParams.update({"font.size": 18})
plt.figure()
plt.plot(
ogs_line.point_data["Distance"] + start_line[0],
ogs_line.point_data["single_species"],
linewidth=4,
color="blue",
label="ogs",
)
plt.plot(
feflow_line.point_data["Distance"] + start_line[0],
feflow_line.point_data["single_species_P_CONC"][:],
linewidth=4,
color="black",
ls=":",
label="FEFLOW",
)
plt.ylabel("concentration [mg/l]")
plt.xlabel("x [m]")
plt.legend(loc="best")
plt.tight_layout()
plt.show()
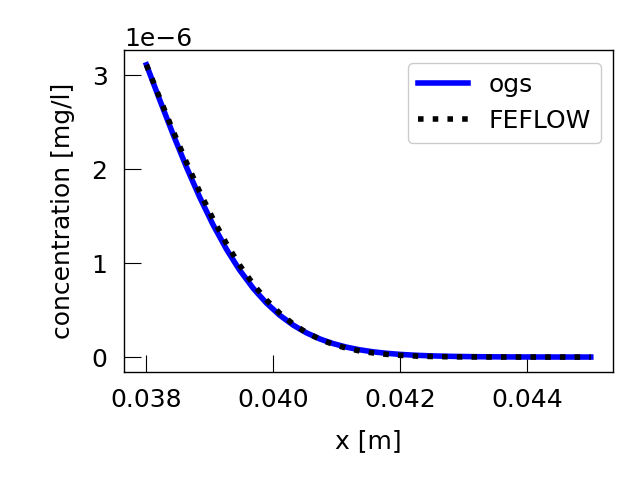
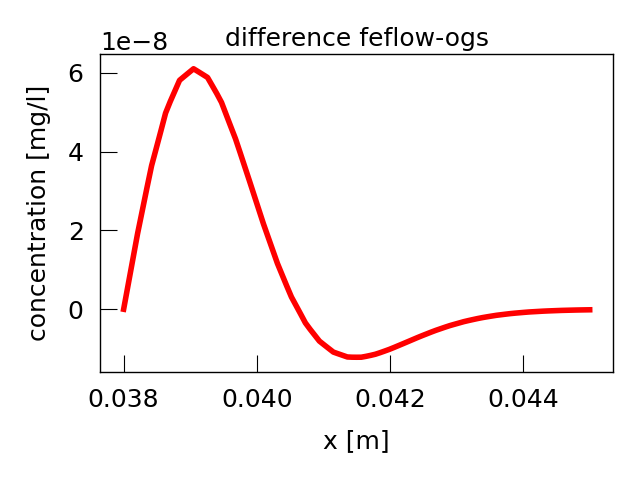
Plot the difference between the FEFLOW and OGS simulation.
plt.figure()
plt.plot(
ogs_line.point_data["Distance"] + start_line[0],
feflow_line.point_data["single_species_P_CONC"]
- ogs_line.point_data["single_species"],
linewidth=4,
color="red",
)
plt.ylabel("concentration [mg/l]")
plt.xlabel("x [m]")
plt.title("difference feflow-ogs")
plt.tight_layout()
plt.show()
Total running time of the script: (0 minutes 3.653 seconds)
