Note
Go to the end to download the full example code. or to run this example in your browser via Binder
Workflow with Feflowlib: Component-transport model - conversion, simulation, postprocessing#
In this example we show how a simple mass transport FEFLOW model can be converted to a pyvista.UnstructuredGrid and then be simulated in OGS with the component transport process.
Necessary imports
import tempfile
import xml.etree.ElementTree as ET
from pathlib import Path
import matplotlib.pyplot as plt
import ogstools as ot
from ogstools.examples import feflow_model_2D_CT_t_560
ot.plot.setup.show_element_edges = True
1. Load a FEFLOW model (.fem) as a FeflowModel object to further work it. During the initialisation, the FEFLOW file is converted.
temp_dir = Path(tempfile.mkdtemp("feflow_test_simulation"))
feflow_model = ot.FeflowModel(
feflow_model_2D_CT_t_560, temp_dir / "2D_CT_model"
)
# name the feflow concentratiob result the same as in OGS for easier comparison
feflow_model.mesh["single_species"] = feflow_model.mesh["single_species_P_CONC"]
concentration = ot.variables.Scalar(
data_name="single_species", output_name="concentration",
data_unit="mg/l", output_unit="mg/l",
) # fmt: skip
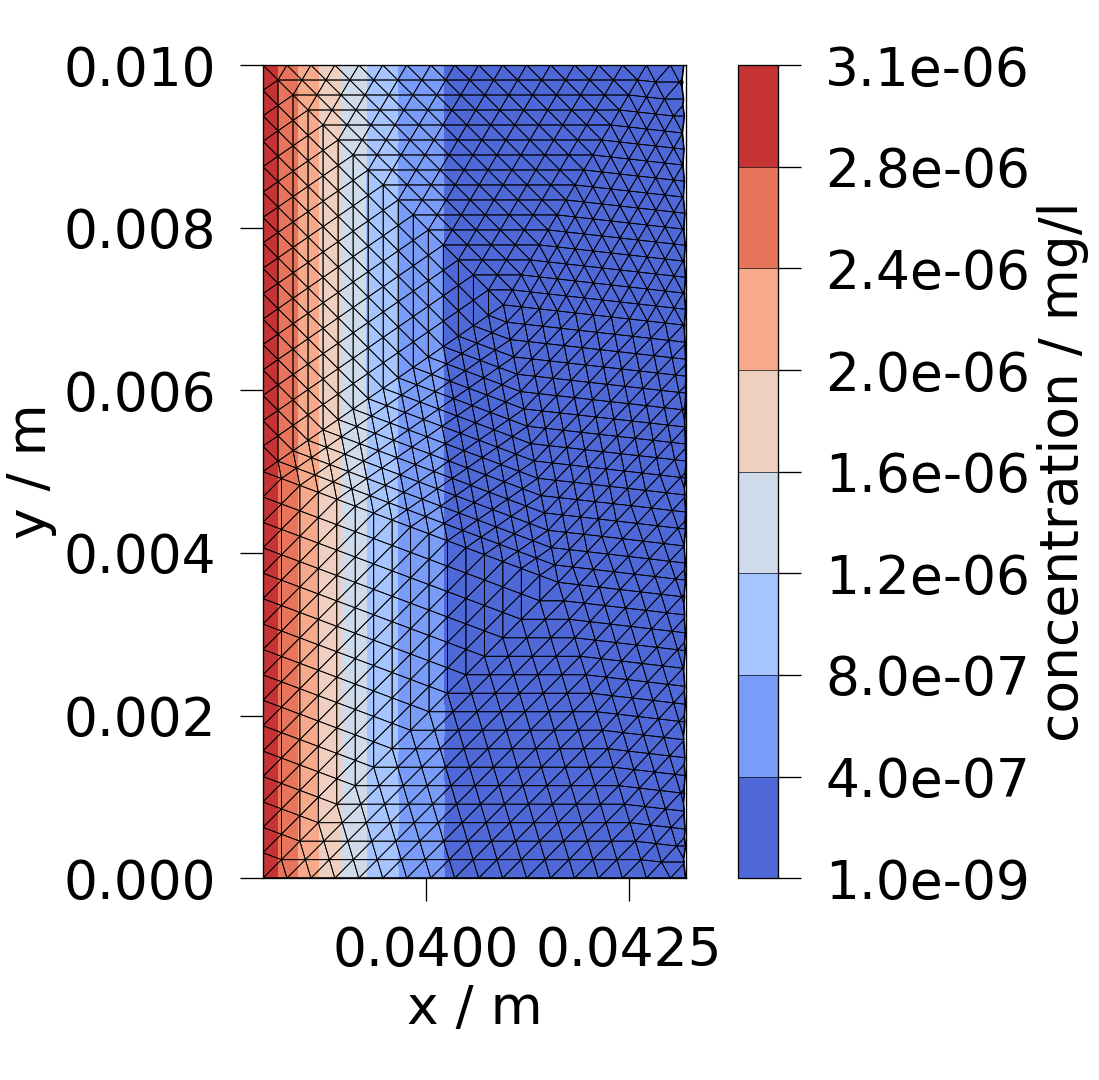
# The original mesh is clipped to focus on the relevant part of it, where
# concentration is larger than 1e-9 mg/l. The rest of the mesh has concentration
# values of 0.
clipped_mesh = feflow_model.mesh.clip_scalar(
scalars="single_species", invert=False, value=1.0e-9
)
ot.plot.contourf(clipped_mesh, concentration)
<Figure size 1099.71x1080 with 2 Axes>
Setup a prj-file to run a OGS-simulation.
time_steps = list(zip([10] * 8, [8.64 * 10**i for i in range(8)], strict=False))
feflow_model.setup_prj(end_time=int(4.8384e07), time_stepping=time_steps)
# Save the model (mesh, subdomains and project file).
feflow_model.save()
# Print the prj-file as an example.
ET.dump(ET.parse(feflow_model.mesh_path.with_suffix(".prj")))
<OpenGeoSysProject>
<meshes>
<mesh>2D_CT_model.vtu</mesh>
<mesh>single_species_P_BC_MASS.vtu</mesh>
</meshes>
<processes>
<process>
<name>CT</name>
<type>ComponentTransport</type>
<coupling_scheme>staggered</coupling_scheme>
<integration_order>2</integration_order>
<specific_body_force>0 0</specific_body_force>
<secondary_variables>
<secondary_variable internal_name="darcy_velocity" output_name="v" />
</secondary_variables>
<process_variables>
<pressure>HEAD_OGS</pressure>
<concentration>single_species</concentration>
</process_variables>
</process>
</processes>
<media>
<medium id="0">
<phases>
<phase>
<type>AqueousLiquid</type>
<properties>
<property>
<name>viscosity</name>
<type>Constant</type>
<value>1</value>
</property>
<property>
<name>density</name>
<type>Constant</type>
<value>1</value>
</property>
</properties>
<components>
<component>
<name>single_species</name>
<properties>
<property>
<name>decay_rate</name>
<type>Constant</type>
<value>0.0</value>
</property>
<property>
<name>pore_diffusion</name>
<type>Constant</type>
<value>3.5999998241701783e-10</value>
</property>
<property>
<name>retardation_factor</name>
<type>Constant</type>
<value>16441.72737282367</value>
</property>
</properties>
</component>
</components>
</phase>
</phases>
<properties>
<property>
<name>porosity</name>
<type>Constant</type>
<value>0.10999999940395355</value>
</property>
<property>
<name>longitudinal_dispersivity</name>
<type>Constant</type>
<value>0.0</value>
</property>
<property>
<name>transversal_dispersivity</name>
<type>Constant</type>
<value>0.0</value>
</property>
<property>
<name>permeability</name>
<type>Constant</type>
<value>1.1574074074074073e-05</value>
</property>
</properties>
</medium>
</media>
<time_loop>
<processes>
<process ref="CT">
<nonlinear_solver>basic_picard</nonlinear_solver>
<convergence_criterion>
<type>DeltaX</type>
<norm_type>NORM2</norm_type>
<reltol>1e-6</reltol>
</convergence_criterion>
<time_discretization>
<type>BackwardEuler</type>
</time_discretization>
<time_stepping>
<type>FixedTimeStepping</type>
<t_initial>0</t_initial>
<t_end>48384000</t_end>
<timesteps>
<pair>
<repeat>10</repeat>
<delta_t>8.64</delta_t>
</pair>
<pair>
<repeat>10</repeat>
<delta_t>86.4</delta_t>
</pair>
<pair>
<repeat>10</repeat>
<delta_t>864.0</delta_t>
</pair>
<pair>
<repeat>10</repeat>
<delta_t>8640.0</delta_t>
</pair>
<pair>
<repeat>10</repeat>
<delta_t>86400.0</delta_t>
</pair>
<pair>
<repeat>10</repeat>
<delta_t>864000.0</delta_t>
</pair>
<pair>
<repeat>10</repeat>
<delta_t>8640000.0</delta_t>
</pair>
<pair>
<repeat>10</repeat>
<delta_t>86400000.0</delta_t>
</pair>
</timesteps>
</time_stepping>
</process>
<process ref="CT">
<nonlinear_solver>basic_picard</nonlinear_solver>
<convergence_criterion>
<type>DeltaX</type>
<norm_type>NORM2</norm_type>
<reltol>1e-6</reltol>
</convergence_criterion>
<time_discretization>
<type>BackwardEuler</type>
</time_discretization>
<time_stepping>
<type>FixedTimeStepping</type>
<t_initial>0</t_initial>
<t_end>48384000</t_end>
<timesteps>
<pair>
<repeat>10</repeat>
<delta_t>8.64</delta_t>
</pair>
<pair>
<repeat>10</repeat>
<delta_t>86.4</delta_t>
</pair>
<pair>
<repeat>10</repeat>
<delta_t>864.0</delta_t>
</pair>
<pair>
<repeat>10</repeat>
<delta_t>8640.0</delta_t>
</pair>
<pair>
<repeat>10</repeat>
<delta_t>86400.0</delta_t>
</pair>
<pair>
<repeat>10</repeat>
<delta_t>864000.0</delta_t>
</pair>
<pair>
<repeat>10</repeat>
<delta_t>8640000.0</delta_t>
</pair>
<pair>
<repeat>10</repeat>
<delta_t>86400000.0</delta_t>
</pair>
</timesteps>
</time_stepping>
</process>
</processes>
<output>
<type>VTK</type>
<prefix>/tmp/tmpinp8_htsfeflow_test_simulation/2D_CT_model</prefix>
<timesteps>
<pair>
<repeat>1</repeat>
<each_steps>1</each_steps>
</pair>
</timesteps>
<variables>
<variable>single_species</variable>
<variable>HEAD_OGS</variable>
</variables>
<fixed_output_times>48384000</fixed_output_times>
</output>
<global_process_coupling>
<max_iter>1</max_iter>
<convergence_criteria>
<convergence_criterion>
<type>DeltaX</type>
<norm_type>NORM2</norm_type>
<reltol>1e-10</reltol>
</convergence_criterion>
<convergence_criterion>
<type>DeltaX</type>
<norm_type>NORM2</norm_type>
<reltol>1e-10</reltol>
</convergence_criterion>
</convergence_criteria>
</global_process_coupling>
</time_loop>
<parameters>
<parameter>
<name>C0</name>
<type>Constant</type>
<value>0</value>
</parameter>
<parameter>
<name>p0</name>
<type>Constant</type>
<value>0</value>
</parameter>
<parameter>
<name>single_species_P_BC_MASS</name>
<type>MeshNode</type>
<mesh>single_species_P_BC_MASS</mesh>
<field_name>single_species_P_BC_MASS</field_name>
</parameter>
</parameters>
<process_variables>
<process_variable>
<name>single_species</name>
<components>1</components>
<order>1</order>
<initial_condition>C0</initial_condition>
<boundary_conditions>
<boundary_condition>
<type>Dirichlet</type>
<mesh>single_species_P_BC_MASS</mesh>
<parameter>single_species_P_BC_MASS</parameter>
</boundary_condition>
</boundary_conditions>
</process_variable>
<process_variable>
<name>HEAD_OGS</name>
<components>1</components>
<order>1</order>
<initial_condition>p0</initial_condition>
</process_variable>
</process_variables>
<nonlinear_solvers>
<nonlinear_solver>
<name>basic_picard</name>
<type>Picard</type>
<max_iter>100</max_iter>
<linear_solver>general_linear_solver</linear_solver>
</nonlinear_solver>
</nonlinear_solvers>
<linear_solvers>
<linear_solver>
<name>general_linear_solver</name>
<lis>-i cg -p jacobi -tol 1e-10 -maxiter 100000</lis>
<eigen>
<solver_type>CG</solver_type>
<precon_type>DIAGONAL</precon_type>
<max_iteration_step>100000</max_iteration_step>
<error_tolerance>1e-10</error_tolerance>
</eigen>
</linear_solver>
</linear_solvers>
</OpenGeoSysProject>
Run the model.
feflow_model.run()
Project file written to output.
Simulation: /tmp/tmpinp8_htsfeflow_test_simulation/2D_CT_model.prj
Status: finished successfully.
Execution took 3.719899892807007 s
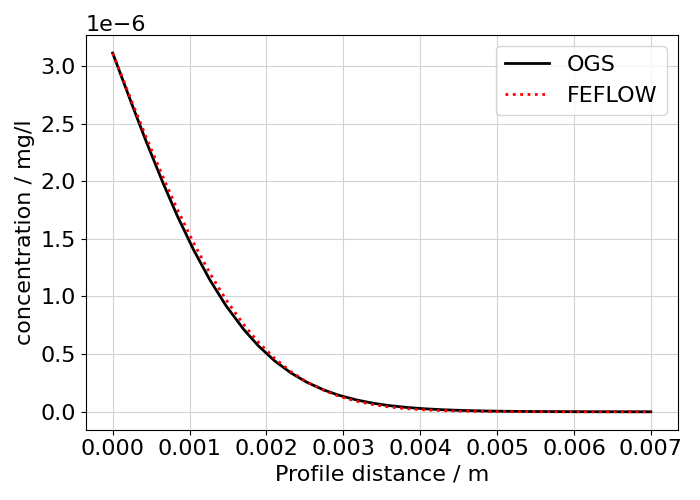
4. Read the last timestep and plot the results along a line on the upper edge of the mesh parallel to the x-axis.
ogs_sim_res = ot.MeshSeries(temp_dir / "2D_CT_model.pvd")[-1]
fig, ax = plt.subplots(1, 1, figsize=(16, 10))
pts = [[0.038 + 1.0e-8, 0.005, 0], [0.045, 0.005, 0]]
for i, mesh in enumerate([ogs_sim_res, feflow_model.mesh]):
sample = mesh.sample_over_line(*pts)
label = ["OGS", "FEFLOW"][i]
ot.plot.line(
sample, concentration, ax=ax, color="kr"[i], label=label, ls="-:"[i]
)
fig.tight_layout()
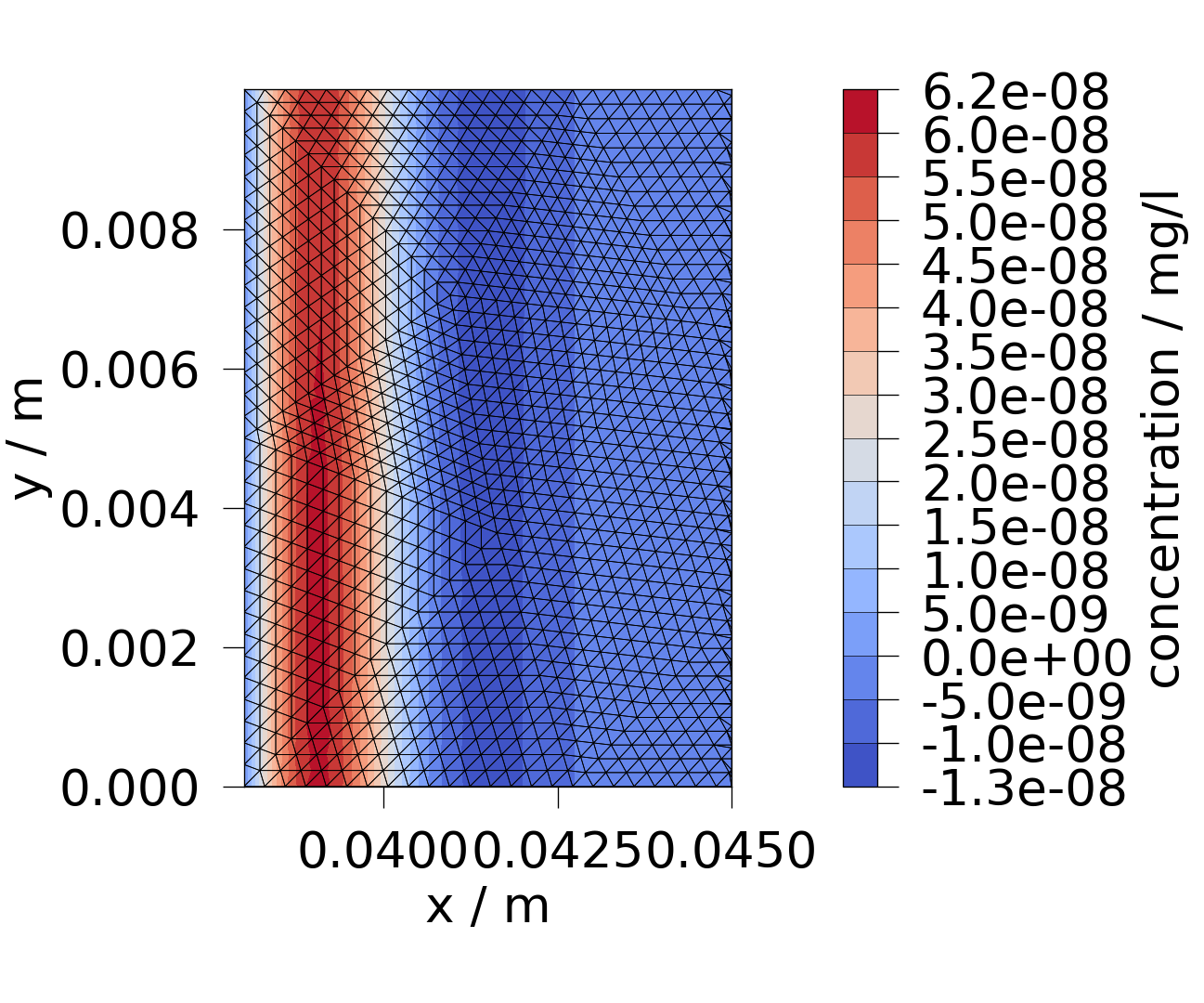
Concentration difference plotted on the mesh.
diff = ot.meshlib.difference(feflow_model.mesh, ogs_sim_res, concentration)
diff_clipped = diff.clip_box([0.038, 0.045, 0, 0.01, 0, 0], invert=False)
fig = ot.plot.contourf(diff_clipped, concentration.difference, fontsize=20)
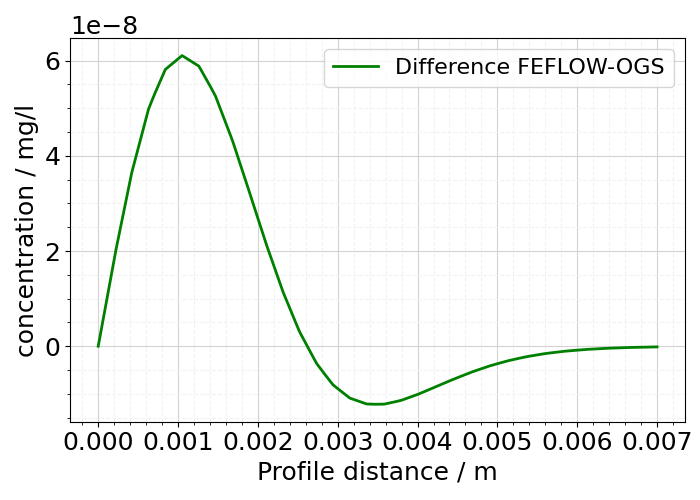
5.1 Concentration difference plotted along a line.
diff_sample = diff.sample_over_line(*pts)
fig = ot.plot.line(
diff_sample, concentration.difference, label="Difference FEFLOW-OGS"
)
fig.tight_layout()
Total running time of the script: (0 minutes 6.403 seconds)

